政治学方法論 II:課題13の解答例
矢内 勇生
2015年7月22日(2015-07-23 改訂)
準備
必要なパッケージを読み込む。インストールの必要があれば各自インストールする。
library("mvtnorm")
library("ggplot2")
library("dplyr")問1. シャツの色の選択
(1)
K <- matrix(c(.2, .2, .6,
.1, .6, .3,
.3, .5, .2),
byrow = TRUE, nrow = 3)
pi_1 <- c(.3, .2, .5)
(pi_2 <- pi_1 %*% K)## [,1] [,2] [,3]
## [1,] 0.23 0.43 0.34(pi_3 <- pi_2 %*% K)## [,1] [,2] [,3]
## [1,] 0.191 0.474 0.335(2)
pi <- c(0, 0, 0)
pi_new <- pi_1
while(sum(abs(pi - pi_new)) > 1e-10) {
pi <- pi_new
pi_new <- pi %*% K
}
pi_new## [,1] [,2] [,3]
## [1,] 0.1827957 0.4946237 0.3225806問2. 夕飯のおかず(豊田 2015: p.64)
この問題の尤度は、 \[y_i | \theta \sim \mathrm{Poisson}(\theta)\] である。
データは、
y <- c(0, 1, 0, 0, 2, 0, 1, 0, 0, 1)
(n <- length(y))## [1] 10である。
(1)
自然な共役事前分布としてガンマ分布を利用すると、事前分布は \[\theta \sim \mathrm{Gamma}(\alpha, \beta)\] となる。ただし、\(\alpha\), \(\beta\) はそれぞれガンマ分布の形状母数と逆尺度 (inverse scale) 母数である。 このとき、ガンマ分布の期待値は、 \[\mathrm{E}(\theta) = \frac{\alpha}{\beta}\] 分散は、 \[\mathrm{var}(\theta) = \frac{\alpha}{\beta^2}\] となる。 したがって、 \[\frac{\alpha}{\beta} = 2\] \[\frac{\alpha}{\beta^2} = 0.8^2\] を解いて、 \[(\alpha, \beta) = (6.25, 3.125)\] となる。
尤度がポアソン分布で事前分布がガンマ分布のとき、事後分布は以下のガンマ分布になる。 \[\theta | y \sim \mathrm{Gamma}(\alpha + \sum y_i, \beta + n)\]
sum(y)## [1] 5だから、\(\theta\) の事後分布は、 \[\theta | y \sim \mathrm{Gamma}(11.25, 13.125)\] である。 この分布から値を1000個抽出し、ヒストグラムにしてみよう。
post_theta_1 <- rgamma(1000, shape = 11.25, rate = 13.125)
hist(post_theta_1, yaxt = "n", col = "gray", nclass = 20,
main = "", xlab = expression(paste("Posterior of ", theta)), ylab = "")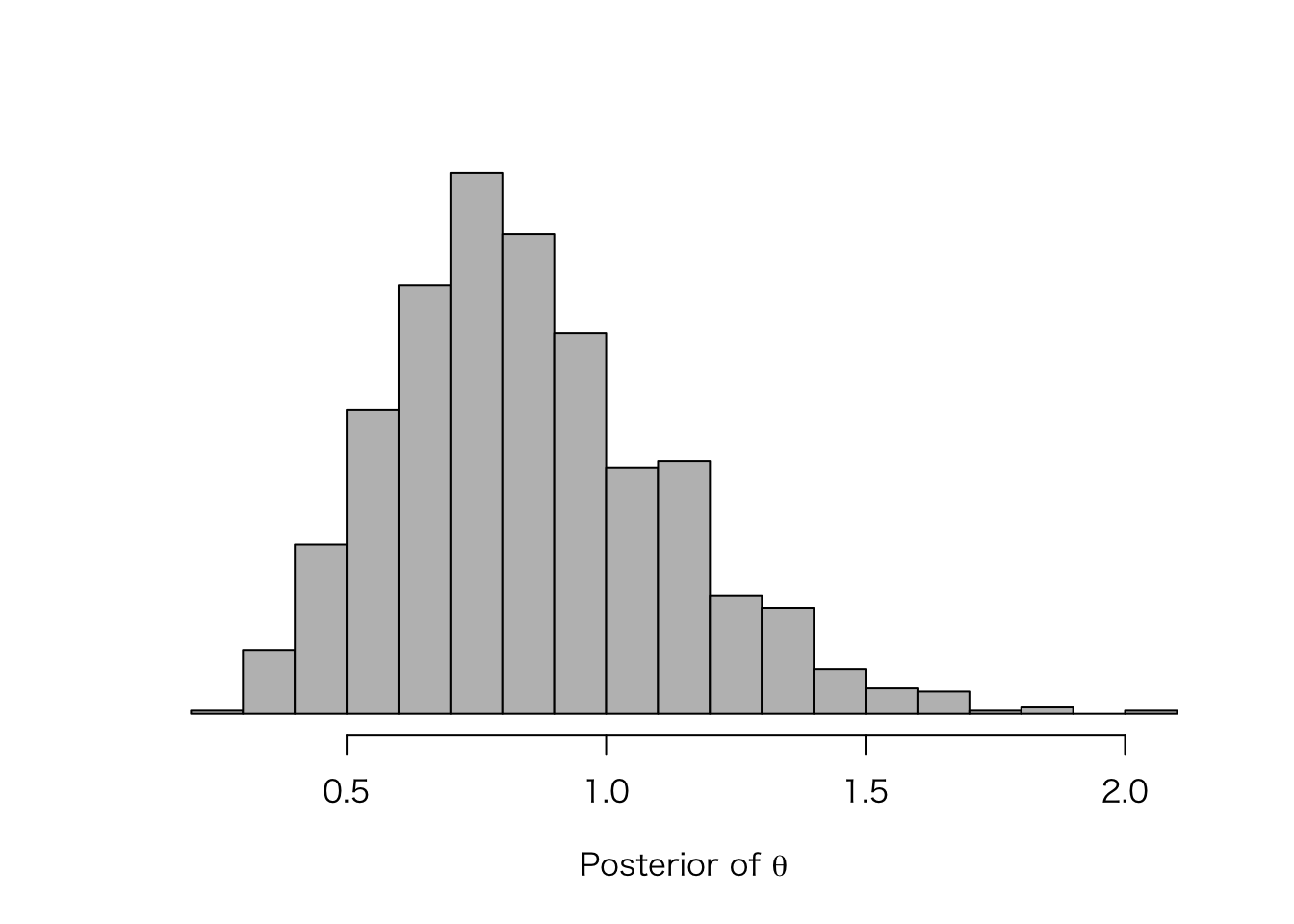
このガンマ分布の最頻値は、 \[\mathrm{mode}(\theta | y) = \frac{11.25 - 1}{13.125} \approx 0.78\] である。\(\theta\) がこの値のとき(最頻値以外の統計量を使ってもかまわない)、Tさんが釣ってくる魚の数が0の確率は、
ppois(0, 0.78)## [1] 0.458406である。
中央値を使うと、
ppois(0, median(post_theta_1))## [1] 0.4382536である。
したがって、妻は約44〜46%の確率で、おかずを用意する必要がある。
\[p(\theta | y) \propto p(y | \theta) p(\theta) = q(\theta |y)\] とすると、 \[p(y | \theta) \propto \prod \theta^{y_i} e^{-\theta},\] \[p(\theta) \propto \theta^{\alpha - 1}e^{-\beta \theta}\] だから、 \[q(\theta | y ) = \theta^{11.25 - 1} e^{-13.125 \theta} = \theta^{10.25} e^{-13.125 \theta}\] である。
非正規化事後分布をRで書くと、
unnorm_dens <- function(theta) {
if (theta < 0) {
return(0)
} else {
return(theta^10.25 * exp(-13.125 * theta))
}
}提案分布に N(1, 0.5) を使い、独立MH法で事後分布をシミュレートする。
fish_sim <- function(n_sims = 100, init = runif(1, 0.5, 1.5)) {
current <- init
res_df <- data.frame(time = 1:n_sims,
post_theta = rep(NA, n_sims))
res_df$post_theta[1] <- current
for (t in 1:(n_sims - 1)){
prop <- rnorm(1, 1, sqrt(.5))
log_r <- log(unnorm_dens(prop)) - log(dnorm(prop, 1, sqrt(.5))) -
log(unnorm_dens(current)) + log(dnorm(current, 1, sqrt(.5)))
prob_mov <- min(1, exp(log_r))
current <- ifelse(runif(1, 0, 1) < prob_mov, prop, current)
res_df$post_theta[t + 1] <- current
}
return(res_df)
}
set.seed(2015-07-22)
sim.1 <- fish_sim(n_sims = 100000)トレースプロットを確認してみよう。
plot(post_theta ~ time, data = sim.1, type = "l")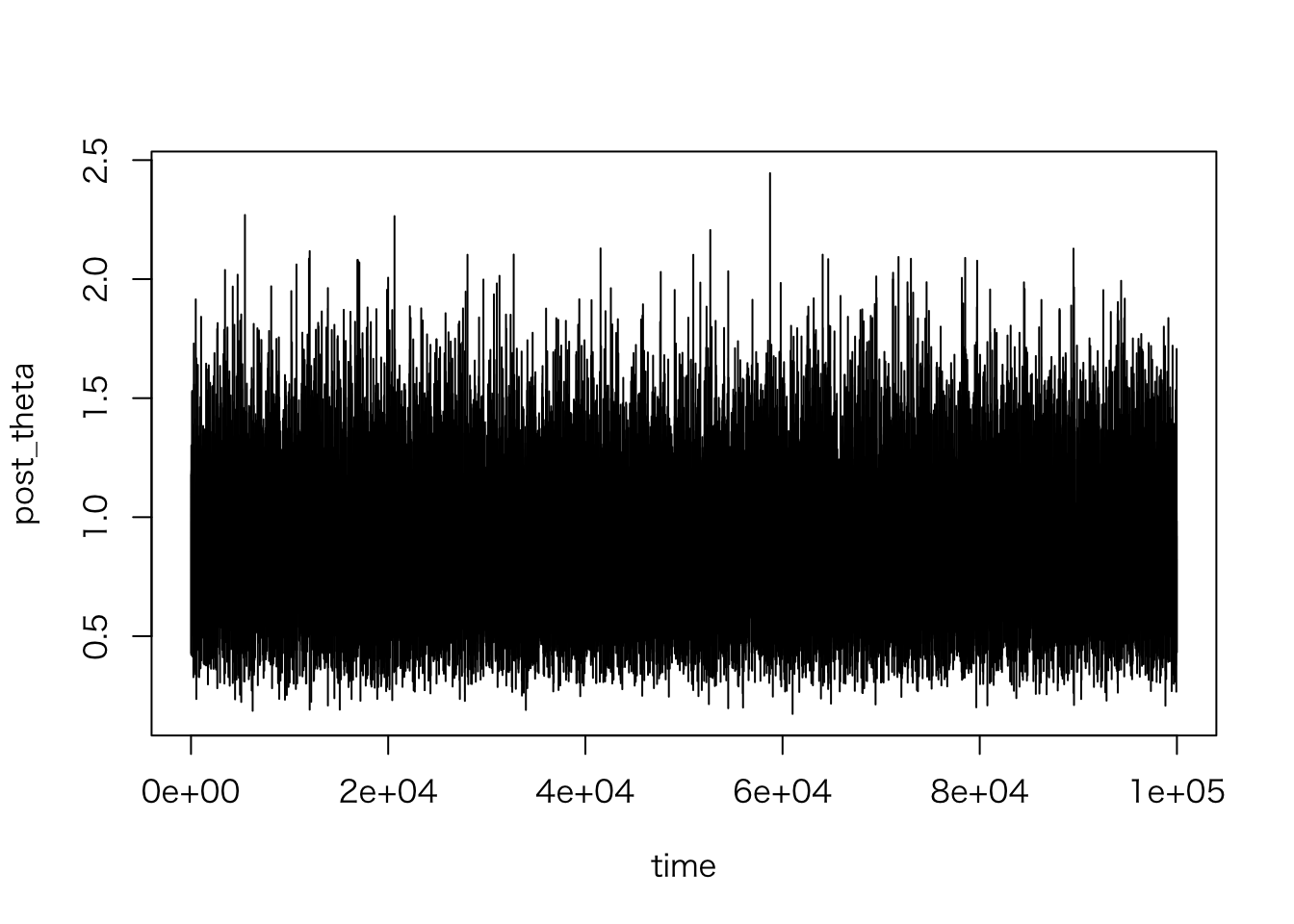
初期の値だけを取り出してみると、
plot(post_theta ~ time, data = sim.1[1:5000,], type = "l")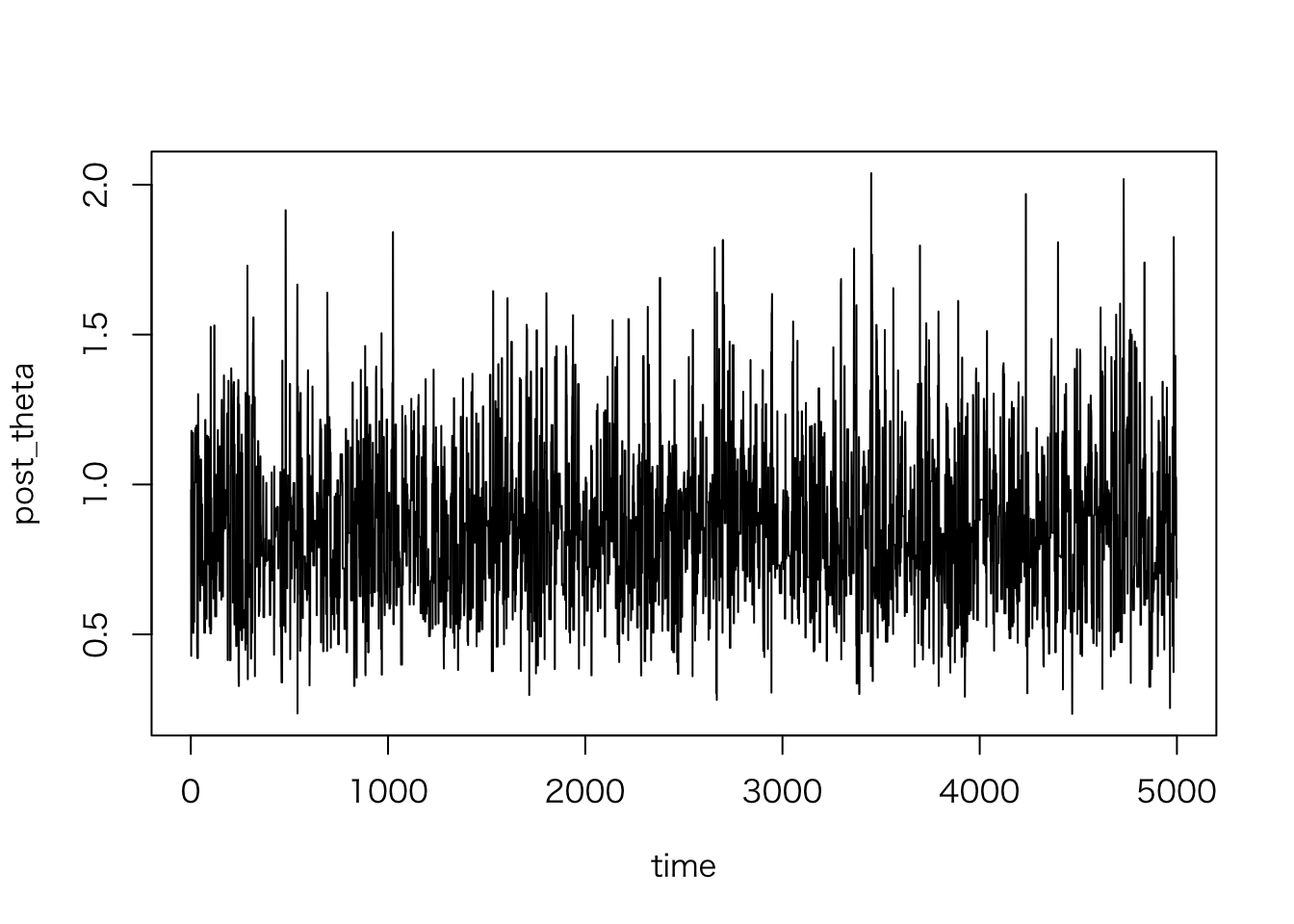
となる。比較的初期の時点で収束しているように見えるので(これは単なる推測)、 最初の4000個の値をバーンインとして捨てることにする。
そうすると、事後分布は、
post_theta_2 <- sim.1$post_theta[-(1:4000)]
hist(post_theta_2, yaxt = "n", col = "gray", nclass = 20,
main = "", xlab = expression(paste("Posterior of ", theta)), ylab = "")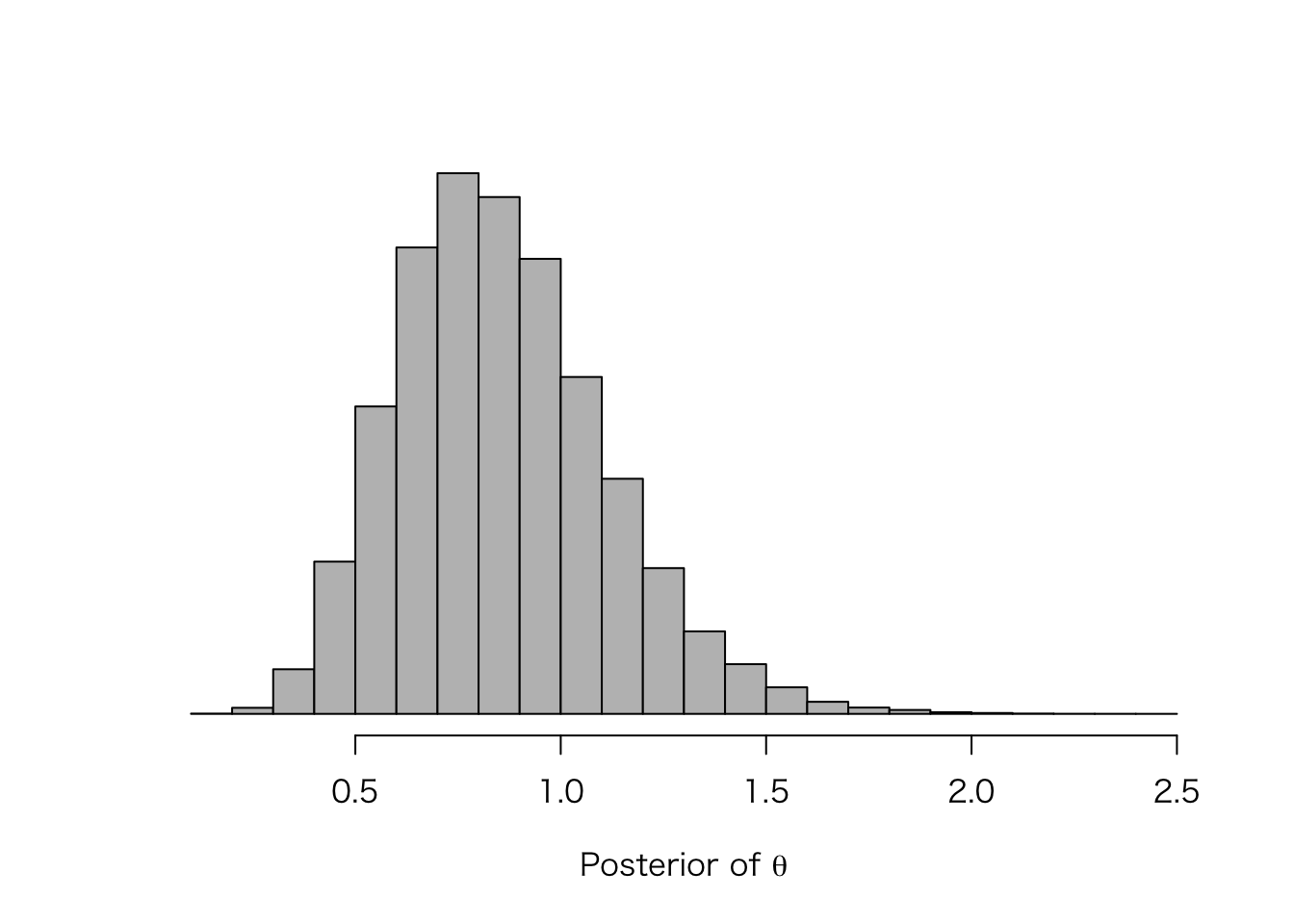
この事後分布の中央値を使って、(1)と同様の確率を求めると、
ppois(0, median(post_theta_2))## [1] 0.4342198したがって、妻は約43%の確率で、おかずを用意する必要がある。
(3)
- の独立MH法で得られた事後分布のヒストグラムの上に、(1)で得られた理論的な事後分布(ガンマ分布の)密度曲線を上書きしてみよう。
hist(post_theta_2, yaxt = "n", col = "gray", nclass = 20, freq = FALSE,
main = "", xlab = expression(paste("Posterior of ", theta)), ylab = "")
curve(dgamma(x, 11.25, 13.125), from = 0, to = 2.5,
add = TRUE, col = "red", lwd = 2)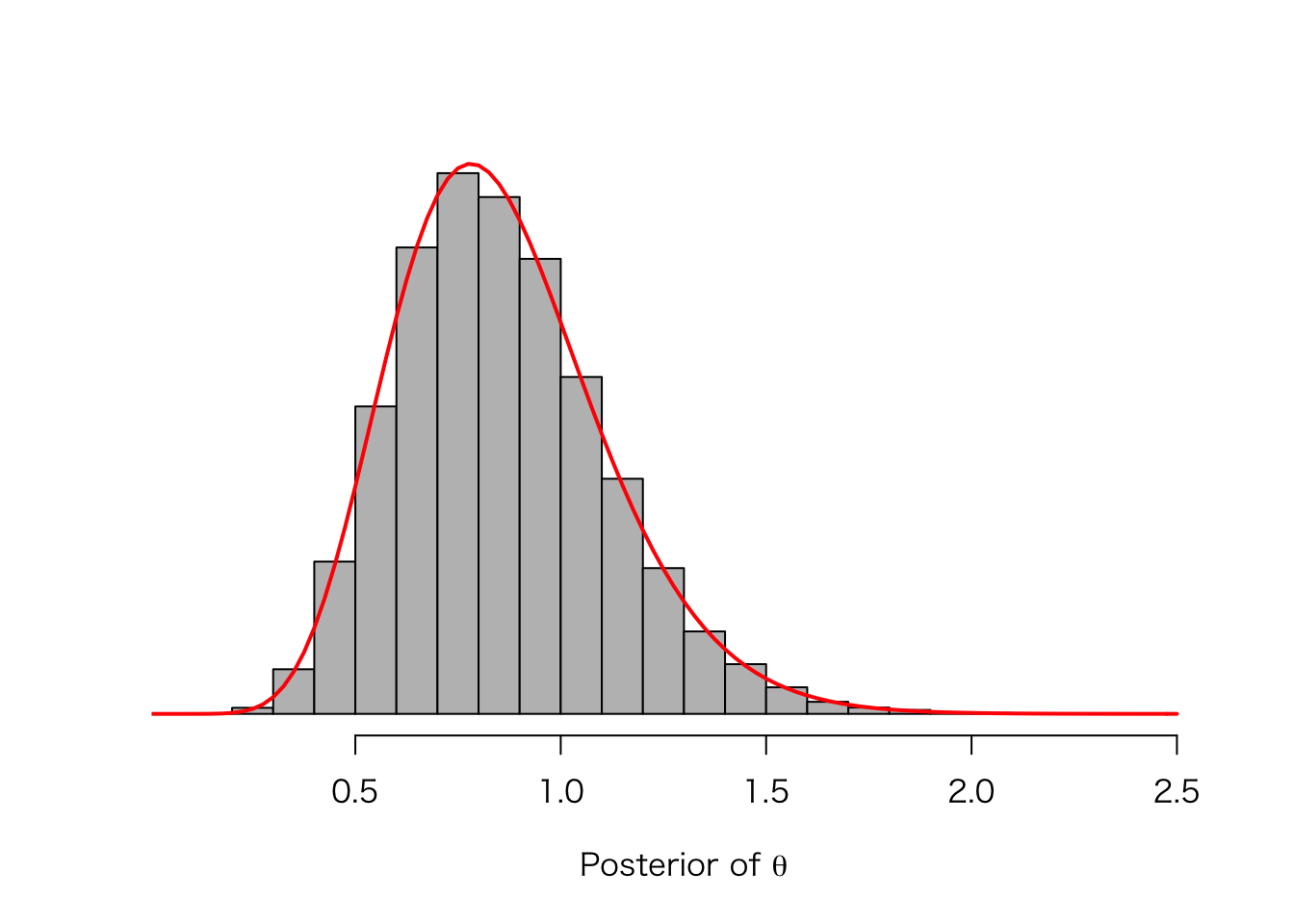
このように、独立MH法でシミュレートした事後分布が、理論的な事後分布に一致することがわかる。
問3. メトロポリス法で生物学的検定実験を分析する。
データ
BDA3, p.74 のデータ (Racine et al. 1986) を使う。
Bio <- data.frame(x = c(-0.86, -0.3, -0.05, 0.73),
n = rep(5, 4),
y = c(0, 1, 3, 5))推定するモデル
実験\(i = 1, \dots, k\) における薬物の投与量 \(x_i\)(単位はlog g/ml)、 動物の個体数 \(n_i\)、死亡した個体数\(y_i\) とする。
核実験内において、各個体が死ぬかどうか独立だと仮定すると、 \[y_i | \theta_i \sim \mathrm{Bin}(n_i, \theta_i)\] となる。ここで、\(\theta_i\) は死亡確率であり、これが推定の対象である。
死亡確率は薬物の投与量によって変化すると想定されるので、これをモデル化する。 ここでは、ロジスティック回帰モデルを使い、 \[\mathrm{logit}(\theta_i) = \alpha + \beta x_i\] あるいは \[\theta_i = \mathrm{logit}^{-1}(\alpha + \beta x_i) = \frac{1}{1 + \exp(-\alpha - \beta x_i)}\] とする。 したがって、このモデルでは、\(\theta_i\) という1つの変量を推定するのではなく、 \(\alpha\) と \(\beta\) という2変量を推定することになる。
尤度、事前分布、事後分布
このモデルの尤度は、 \[p(y_i | \alpha, \beta, n_i, x_i) = \theta_i^{y_i} (1 - \theta_i)^{n_i - y_i}\] である。
したがって、事後分布は、 \[p(\alpha, \beta | y, n, x) \propto p(\alpha, \beta | n, x)p(y | \alpha, \beta, n, x) \propto p(\alpha, \beta) \prod_{i=1}^k p(y_i | \alpha, \beta, n_i, x_i)\] となる。
\(\alpha\) と \(\beta\) についての事前情報がないので、無情報事前分布を使うことにする。 \(p(\alpha, \beta) \propto 1\) とすると、事後分布は、 \[p(\alpha, \beta | y, n, x) \propto \prod_{i=1}^k p(y_i | \alpha, \beta, n_i, x_i)\] となる。 したがって、非正規化事後分布は \[q(\alpha, \beta | y, n, x) = \prod_{i=1}^k p(y_i | \alpha, \beta, n_i, x_i) = \prod \theta_i^{y_i} ( 1 - \theta_i)^{n_i - y_i}\] である。
メトロポリス法による事後分布のシミュレーション
まず、非正規化事後分布の関数を定義する。
invlogit <- function(x) {
return(1 / (1 + exp(-x)))
}
ln_unnorm_post <- function(alpha, beta, data = Bio) {
theta <- invlogit(alpha + beta * data$x)
lik <- log(theta^data$y * (1 - theta)^{data$n - data$y})
return(sum(lik)) ## return log of unnormalized posterior
}\(\alpha\) と \(\beta\) の事後分布をメトロポリス法でシミュレートしよう。
bio_sim <- function(n_sims = 100, init = rnorm(2), sigma = 2) {
alpha_c <- init[1]
beta_c <- init[2]
res_df <- data.frame(time = 1:n_sims,
post_alpha = rep(NA, n_sims),
post_beta = rep(NA, n_sims))
res_df$post_alpha[1] <- alpha_c
res_df$post_beta[1] <- beta_c
Sigma <- sigma * matrix(c(1, .5, .5, 4), nrow = 2)
for (t in 2:n_sims){
prop <- rmvnorm(1, mean = c(alpha_c, beta_c), sigma = Sigma)
alpha_p <- prop[1, 1]
beta_p <- prop[1, 2]
log_r <- ln_unnorm_post(alpha = alpha_p, beta = beta_p) -
ln_unnorm_post(alpha = alpha_c, beta = beta_c)
prob_mov <- min(1, exp(log_r))
if (is.na(prob_mov)) prob_mov <- 0
if (runif(1, 0, 1) < prob_mov) {
alpha_c <- alpha_p
beta_c <- beta_p
}
res_df$post_alpha[t] <- alpha_c
res_df$post_beta[t] <- beta_c
}
return(res_df)
}
set.seed(2015-07-22)
sim.2 <- bio_sim(n_sims = 100000)\(\alpha\), \(\beta\) それぞれについてトレースプロットを描いてみよう。
plot(post_alpha ~ time, data = sim.2, type = "l")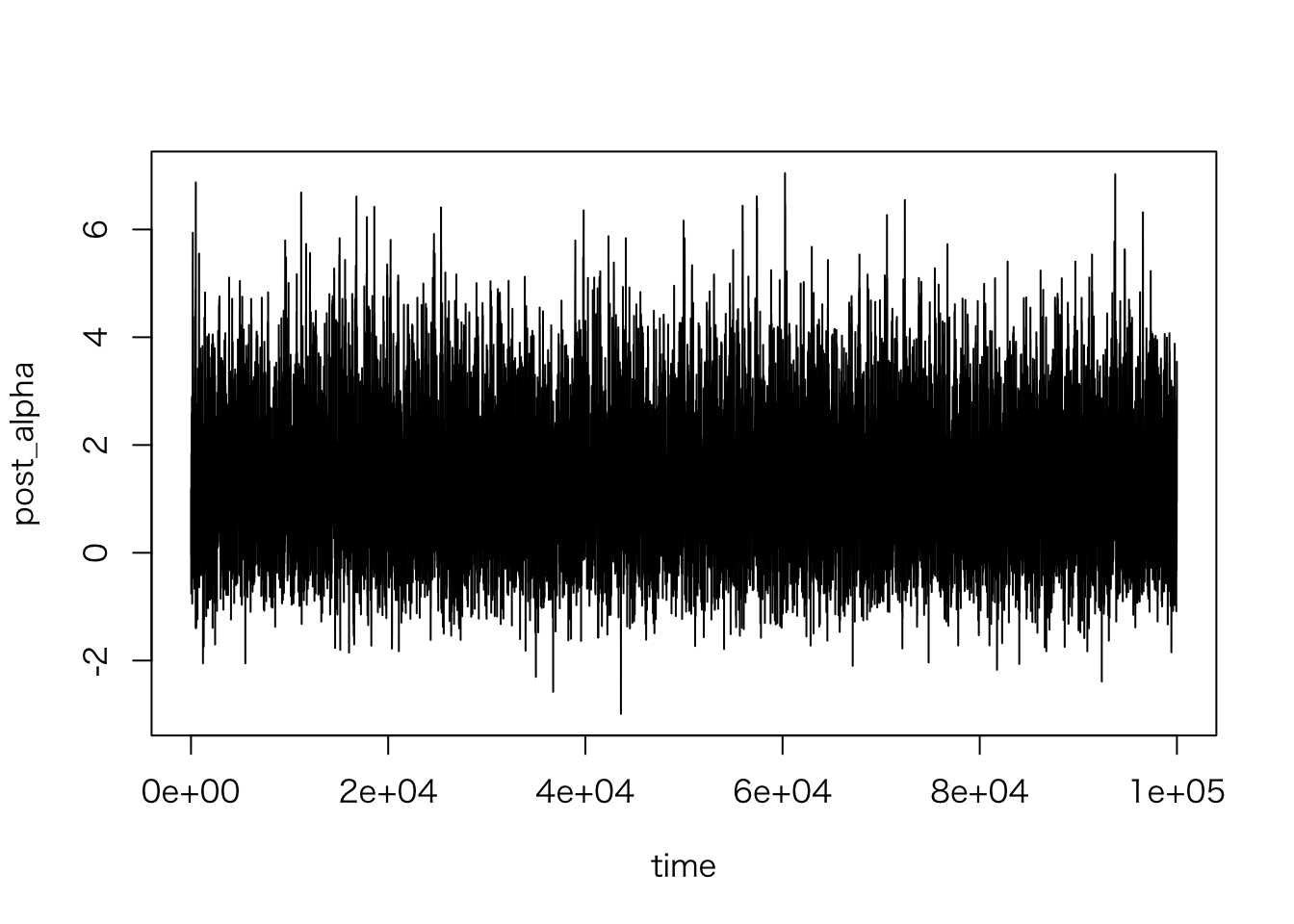
plot(post_beta ~ time, data = sim.2, type = "l")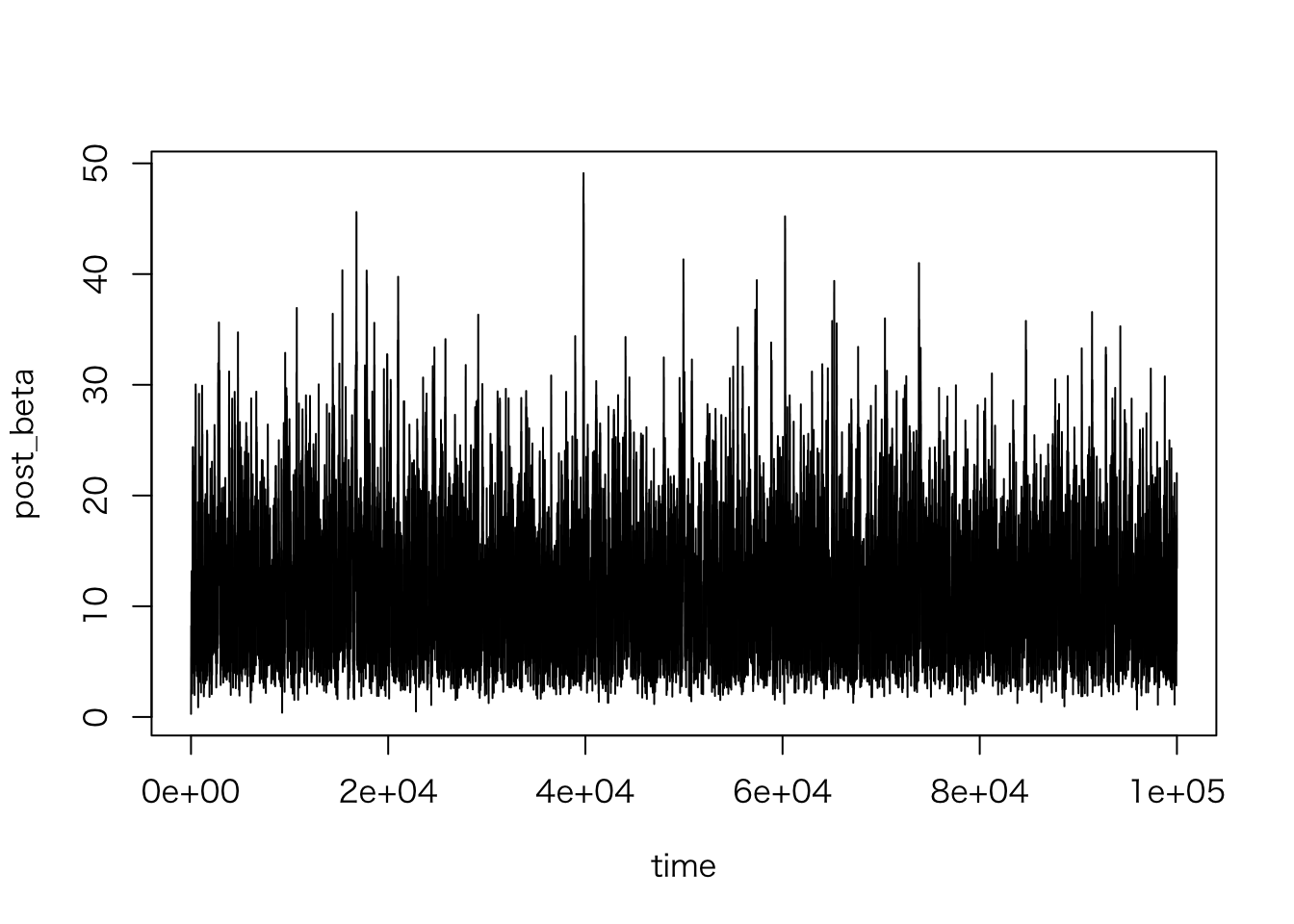
初期だけ取り出してみよう。
plot(post_alpha ~ time, data = sim.2[1:20000,], type = "l")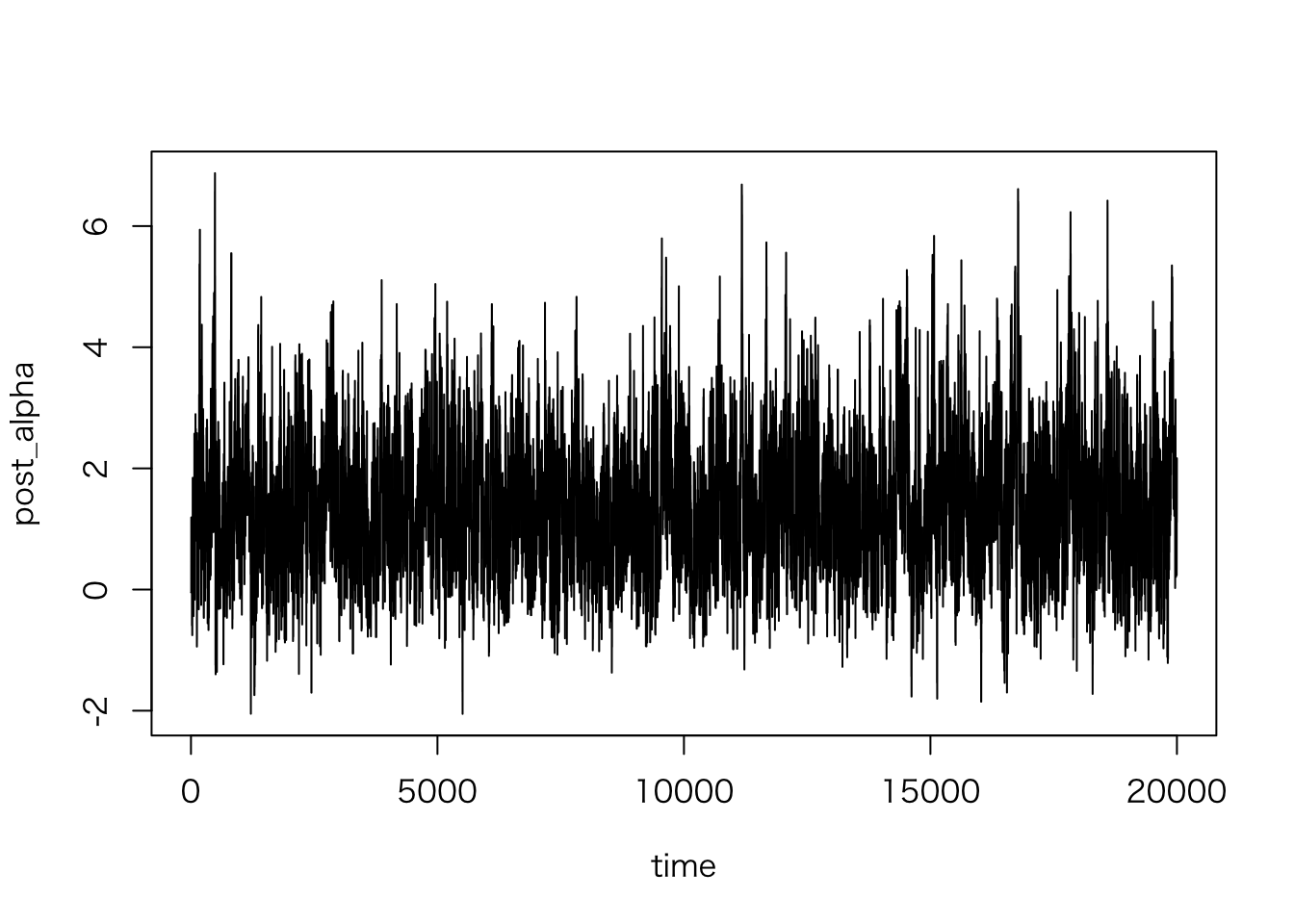
plot(post_beta ~ time, data = sim.2[1:20000,], type = "l")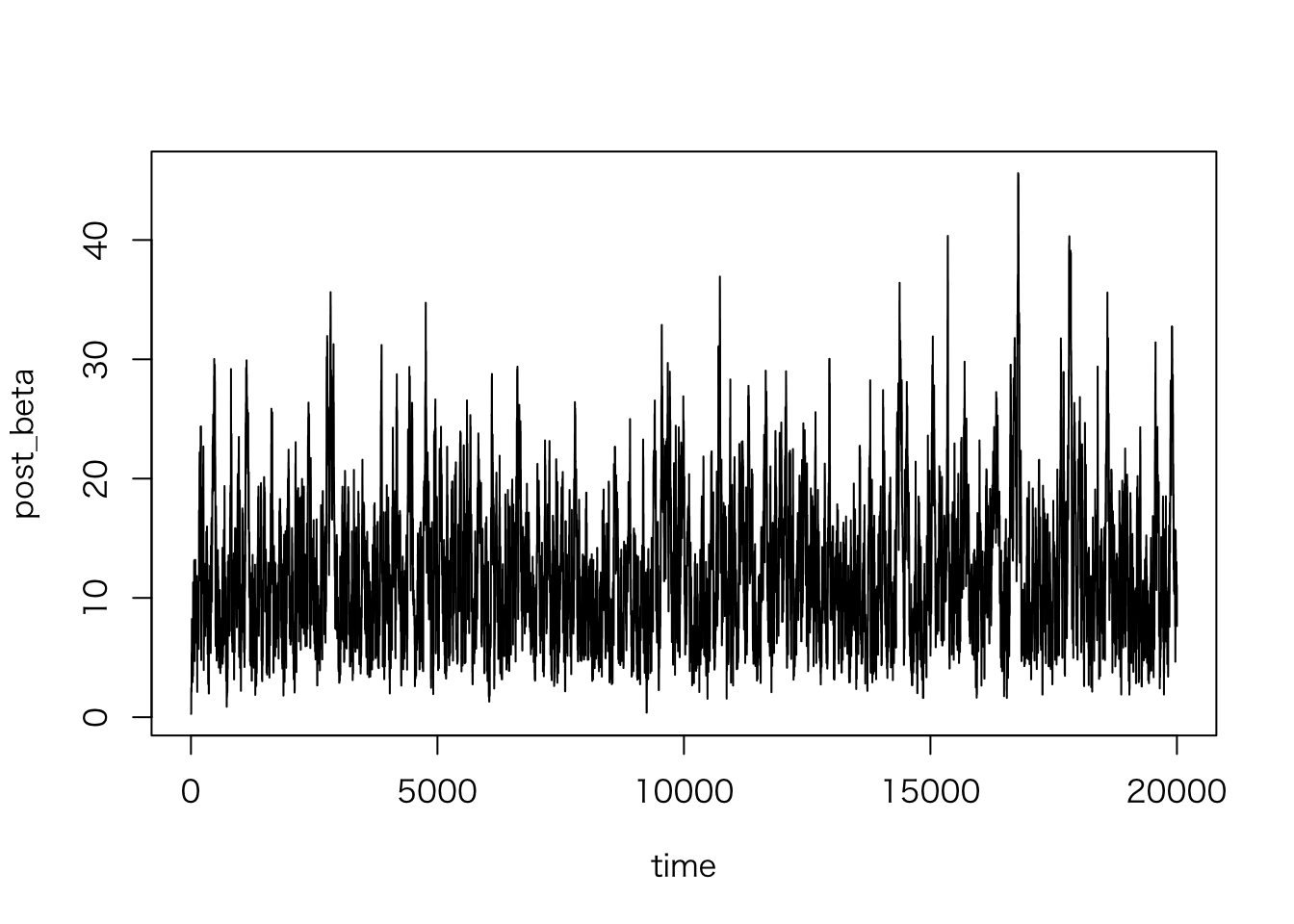
全体としてみるとはっきりしたトレンドはなさそうだが、初期のトレースはやや不安定なので、 初期の20,000 個はバーンインとして破棄しよう。
post_alpha <- sim.2$post_alpha[-(1:20000)]
post_beta <- sim.2$post_beta[-(1:20000)]
Post <- data.frame(alpha = post_alpha, beta = post_beta)事後分布から1000組抽出して散布図にしてみよう。
bio.post <- ggplot(sample_n(Post, 1000), aes(x = alpha, y = beta))
bio.post + geom_point() + xlim(-5, 10) + ylim(-10, 40) +
ggtitle("1000 draws from the posterior")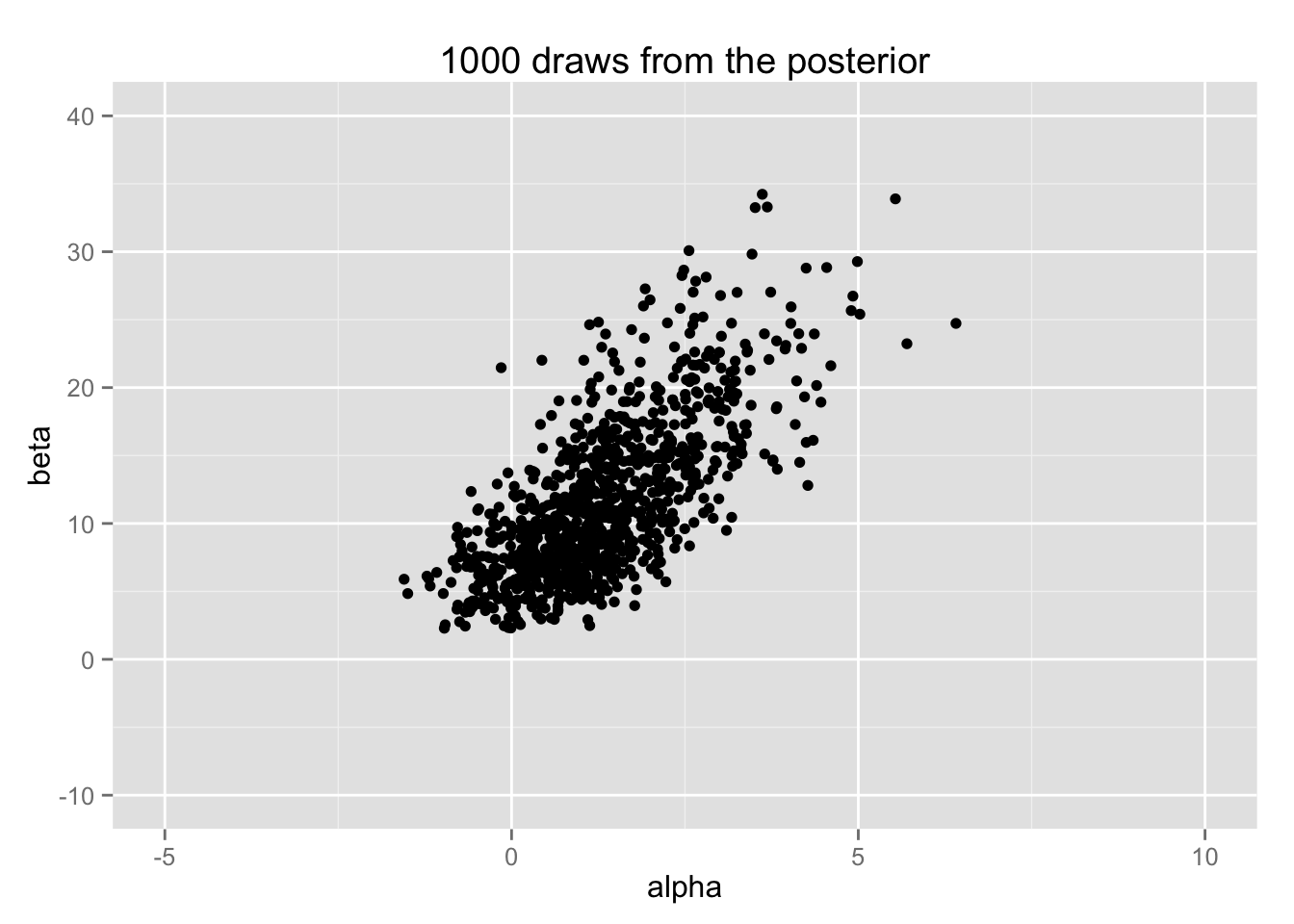
抽出された順にトレースする。
plot(beta ~ alpha, data = Post, type = "l")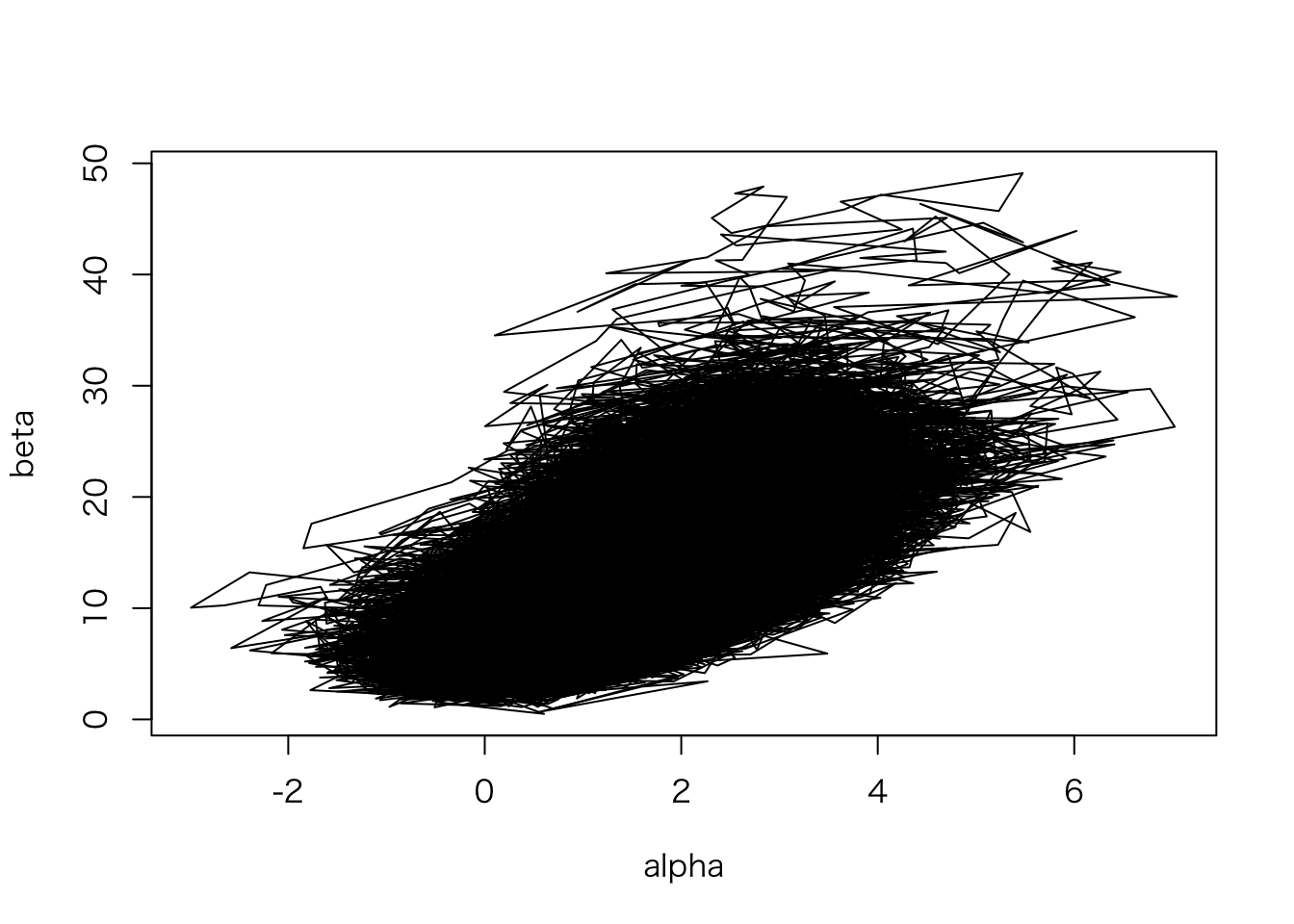
一部だけ取り出してみる。
plot(beta ~ alpha, data = slice(Post, 1:1000), type = "l")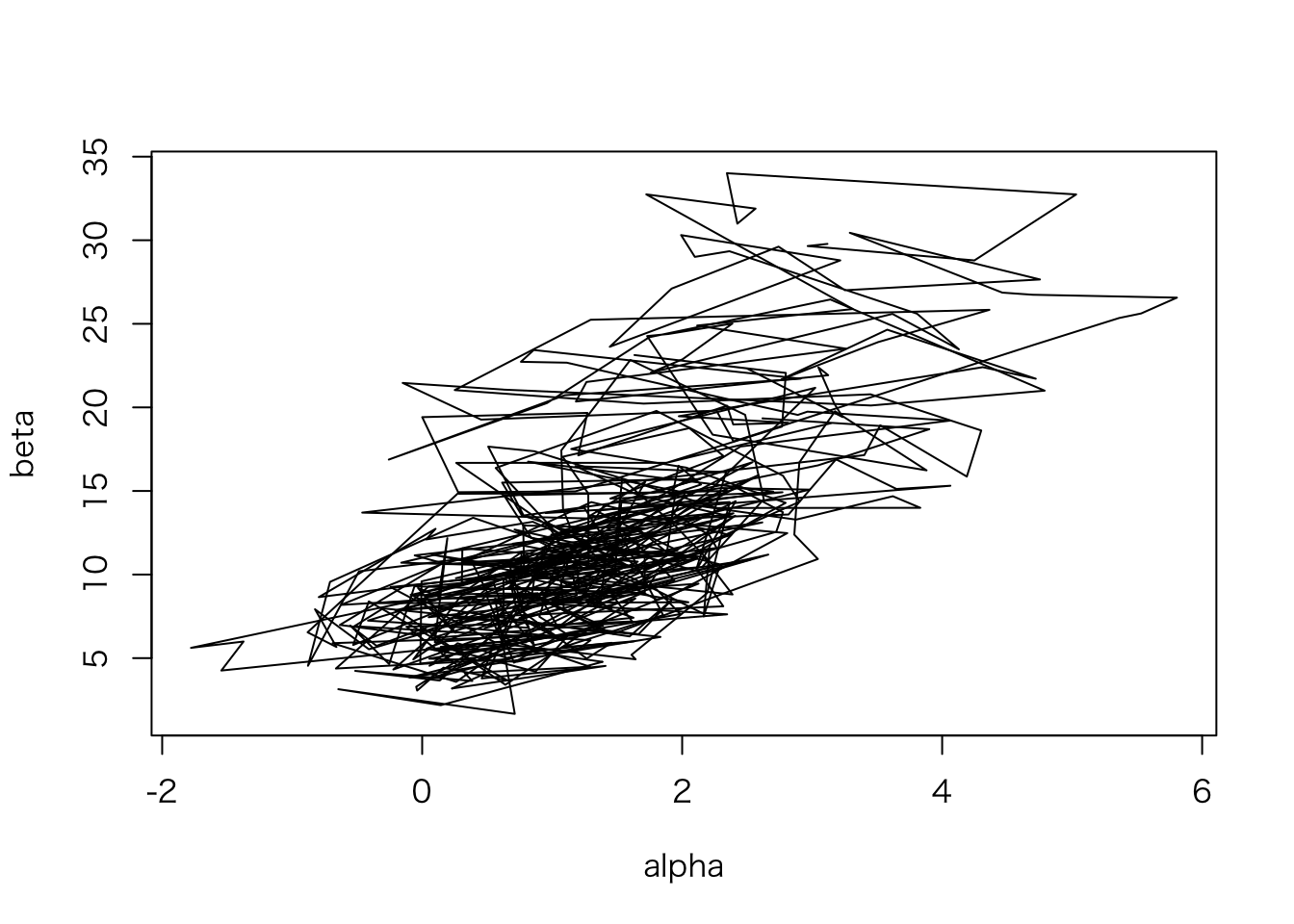
\(\alpha\), \(\beta\) のヒストグラムを描いてみよう。
bio.post.alpha <- ggplot(Post, aes(x = alpha, y = ..density..)) +
geom_histogram(binwidth = 0.25)
bio.post.alpha + ggtitle("Posterior marginal of alpha")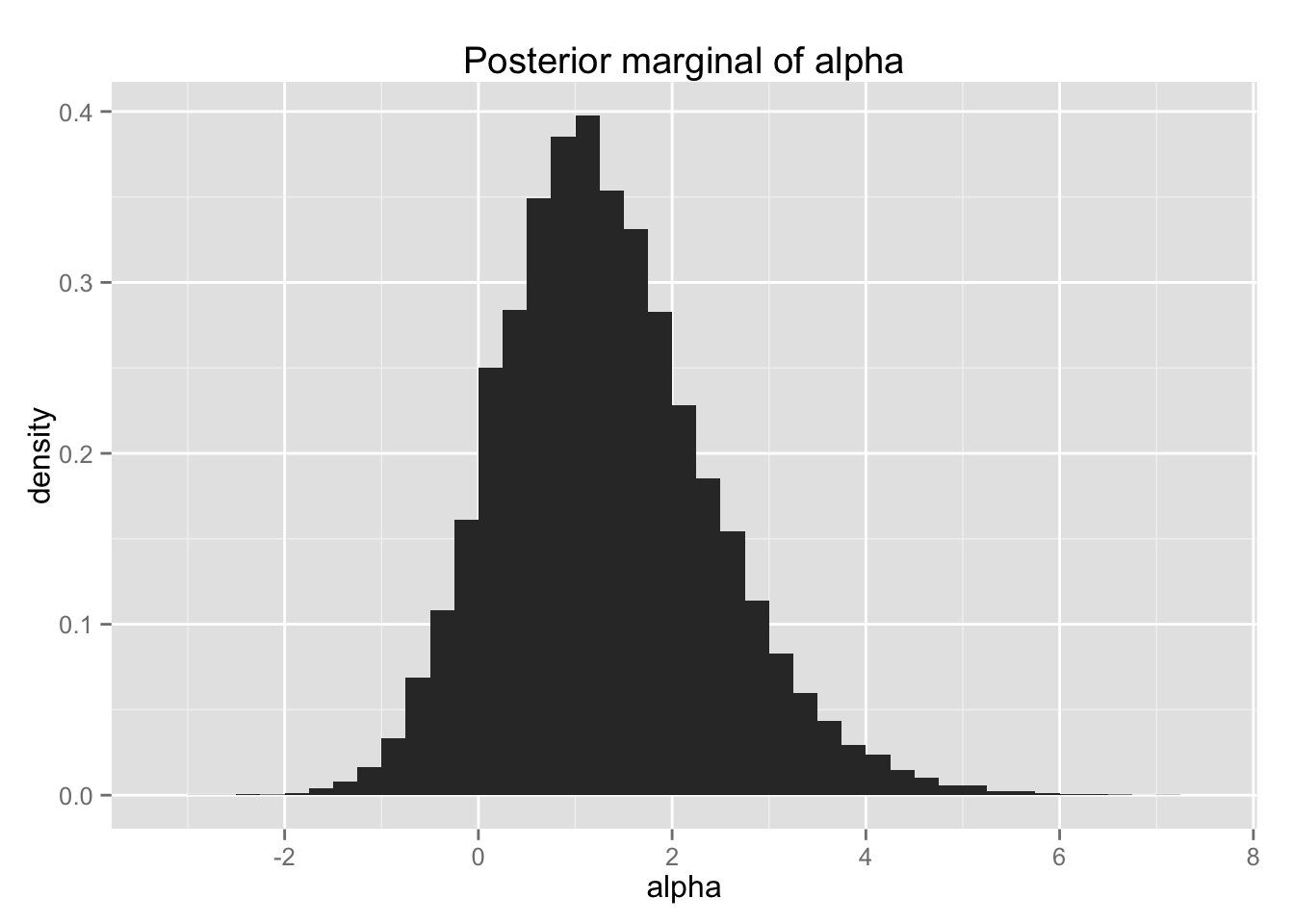
bio.post.beta <- ggplot(Post, aes(x = beta, y = ..density..)) +
geom_histogram(binwidth = 1)
bio.post.beta + ggtitle("Posterior marginal of beta")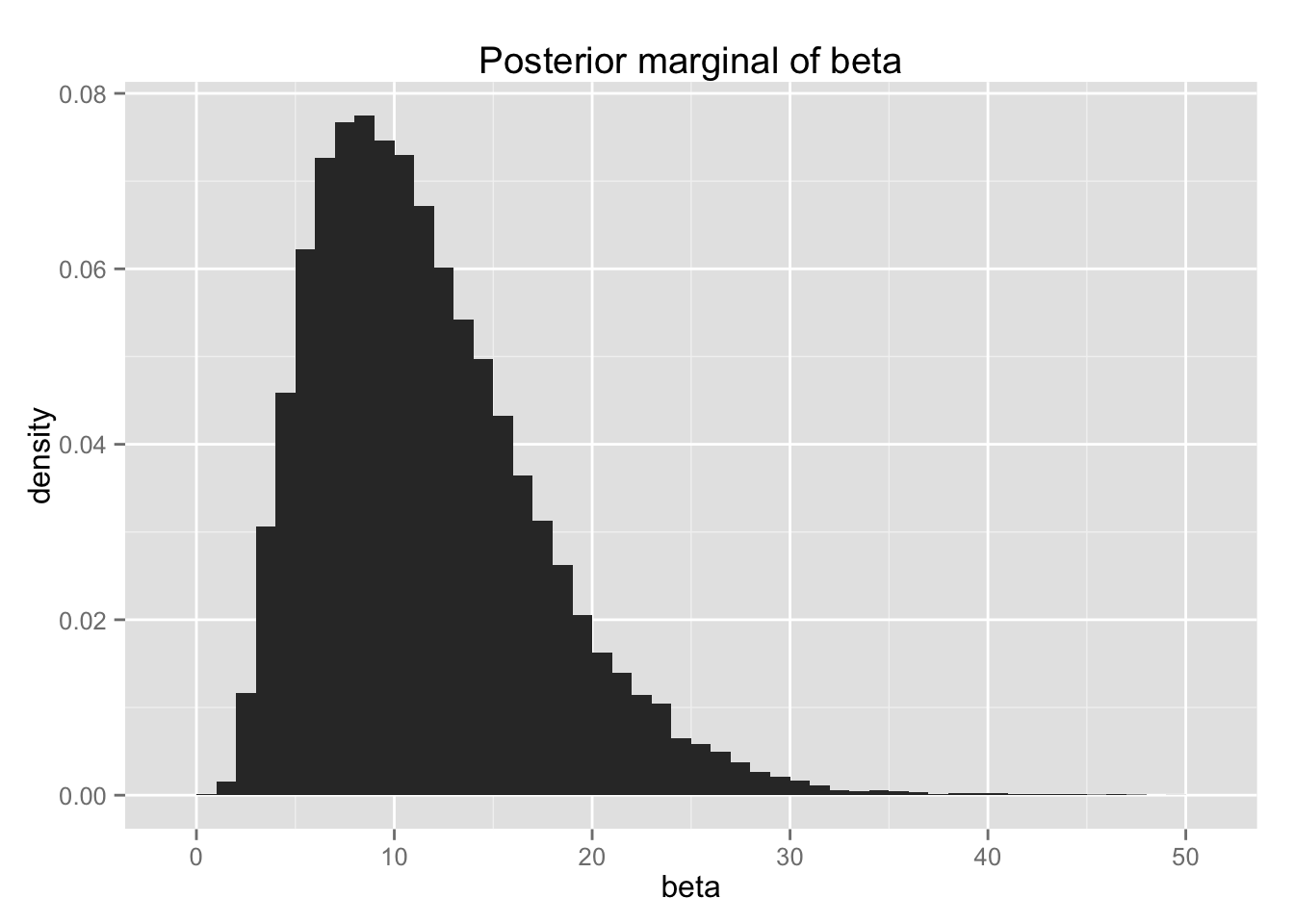
薬物が死亡率に正の影響を与えるのは、\(\beta >0\) のときである。 \(\beta | y > 0\) となる確率は、
sum(post_beta > 0) / length(post_beta)## [1] 1である。
LD50 の事後分布
被験体の50%が死亡する確率 LD50 の事後分布を知りたいとする。 死亡確率が50%、つまり\(\theta_i = 0.5\) だから、 \[\mathrm{logit}^{-1}(\alpha + \beta x_i) = 0.5\] である。ロジットの逆関数が0.5 になるのは、\(\alpha + \beta x_i = 0\) のとき、すなわち、\(x_i = -\alpha / \beta\) である。したがって、私たちが知りたいのは、\(-\alpha / \beta\) の事後分布である。
ただし、薬物が死亡確率を上げない場合、死亡率を50%にする薬物量を考える意味がわからないので、\(\beta > 0\) の場合のみを考える。
この事後分布は、以下のようになる。
bio.ld50 <- ggplot(subset(Post, beta > 0), aes(x = -(alpha / beta))) +
geom_histogram(aes(y = ..density..))
bio.ld50 + ggtitle("Draws from the posterior of the LD50") + xlab("LD50")## stat_bin: binwidth defaulted to range/30. Use 'binwidth = x' to adjust this.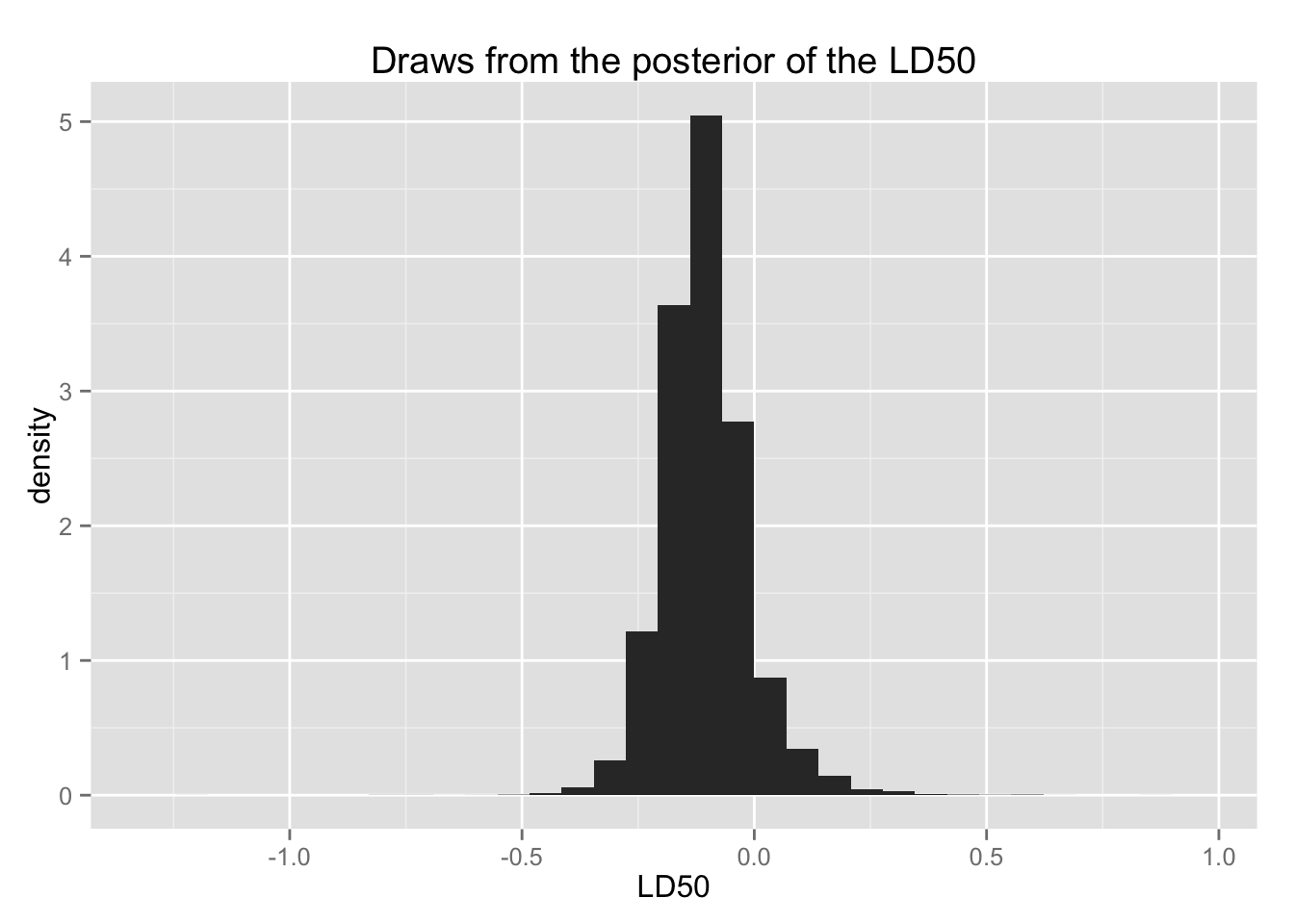
LD50の95%事後区間は、
quantile(-(post_alpha / post_beta), c(.025, .975))## 2.5% 97.5%
## -0.2731086 0.1044055である。 薬物の投与量は対数で与えられていたので、元のスケールに戻すと、
exp(quantile(-(post_alpha / post_beta), c(.025, .975)))## 2.5% 97.5%
## 0.7610102 1.1100505となる。