7  シミュレーションを利用して大数の法則を理解する

今回の目標

7.1 準備

必要なパッケージを読み込む。

library(tidyverse)

## 図のなかで日本語を使えるようにする
## フォントの設定はお好みで
## （Unix/Linux ではIPAexフォントのインストールが必要かも）
if (.Platform$OS.type == "windows") { # Windows
  library(fontregisterer)
  my_font <- "Yu Gothic"
} else if (capabilities("aqua")) { # macOS
  my_font <- "HiraginoSans-W3"
} else { # Unix/Linux
  my_font <- "IPAexGothic"
}
theme_set(theme_gray(base_size = 9,
                     base_family = my_font))

7.2 大数の法則 (Law of Large Numbers; LLN)

「公正な（表が出る確率と裏が出る確率が等しい）」コインを使って、大数の法則のシミュレーションを行う。

コイン投げは、

coin <- c("表", "裏")
sample(coin, size = 1)
[1] "表"

で実行する。

これを1回だけ実行したとき、表の比率は、

  1. 表が出れば1
  2. 裏が出れば0

である。コイン投げの回数が少ないと、表が出る比率は真の比率である0.5に近くなるとは限らない。

しかし、大数の法則によると、コインを投げる回数を十分大きくすると、表の比率は0.5 に近づくはずである。Rを使って確かめてみよう。

まず、コインを投げる回数 n_flips を決める。500に設定してみよう。

n_flips <- 500

次に、結果を記録する容器（ベクトル）を用意する。

ratio_1 <- rep(NA, n_flips)

準備ができたので、n_flips回コイン投げを行い、それぞれのコイン投げが終わった時点での表の比率を計算する。

coins_1 <- sample(coin, size = n_flips, replace = TRUE)
for (i in 1:n_flips) {
  n_head <- sum(coins_1[1:i] == "表") # i回目までに何回表が出たか数える
  ratio_1[i] <- n_head / i            # i回目までの表の比率を計算して記録する
}

これで、ratio_1 に結果が記録された。確認のため、最初の5回分を表示してみよう。

ratio_1[1:5]
[1] 1 1 1 1 1

結果を図示しよう。

df2 <- tibble(N = 1 : n_flips,
              ratio_1 = ratio_1)
p1 <- ggplot(df2, aes(x = N, y = ratio_1)) +
  geom_hline(yintercept = 0.5, 
             linetype = "dashed") +
  geom_line(color = "dodgerblue") +
  labs(x = "試行回数", 
       y = "表の割合")  
plot(p1)

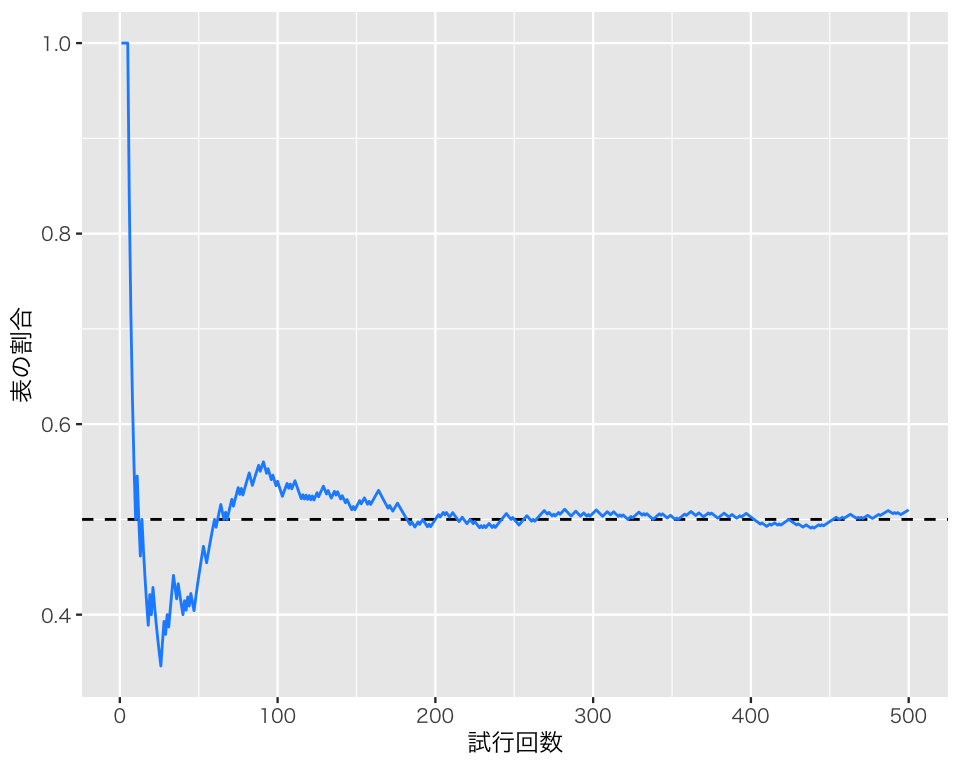
比率が少しずつ0.5に近づいていくことがわかる。

もう1度やってみよう。

ratio_2 <- rep(NA, n_flips)
coins_2 <- sample(coin, size = n_flips, replace = TRUE)
for (i in 1 : n_flips) {
  n_head <- sum(coins_2[1:i] == "表") # i回目までに何回表が出たか数える
  ratio_2[i] <- n_head / i            # i回目までの表の比率を計算して記録する
}
df2$ratio_2 <- ratio_2
p2 <- ggplot(df2, aes(x = N, y = ratio_2)) +
  geom_hline(yintercept = 0.5,
             linetype = "dashed") +
  geom_line(color = "dodgerblue") +
  labs(x = "試行回数", 
       y = "表の割合")  
plot(p2)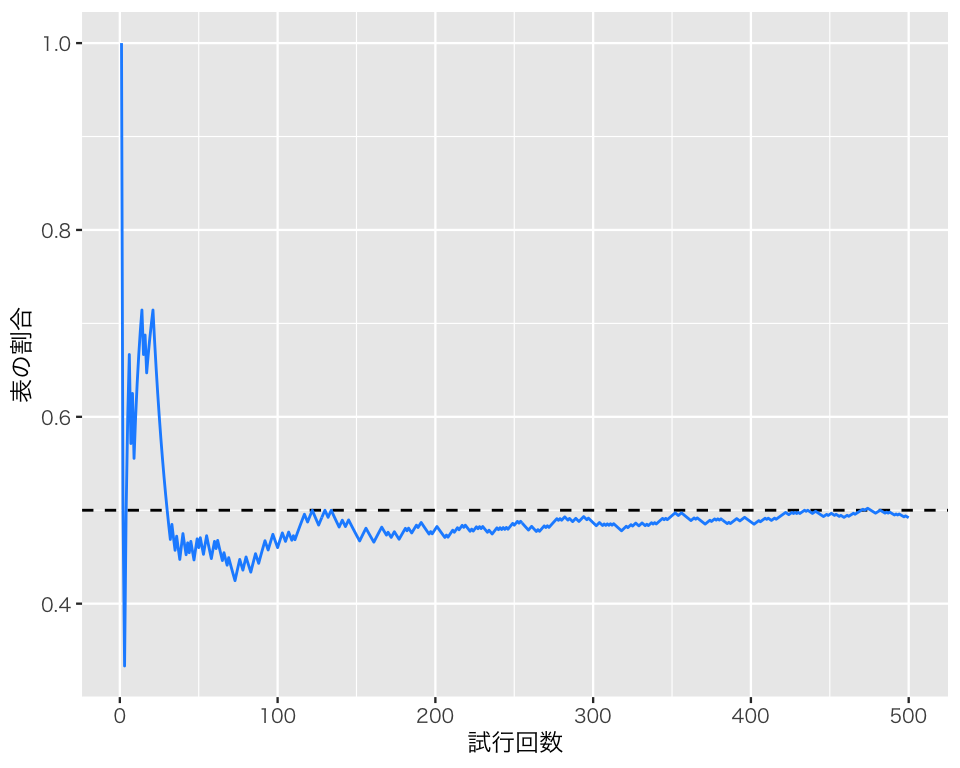

もう1度やってみよう。

ratio_3 <- rep(NA, n_flips)
coins_3 <- sample(coin, size = n_flips, replace = TRUE)
for (i in 1 : n_flips) {
  n_head <- sum(coins_3[1:i] == "表") # i回目までに何回表が出たか数える
  ratio_3[i] <- n_head / i            # i回目までの表の比率を計算して記録する
}
df2$ratio_3 <- ratio_3
p3 <- ggplot(df2, aes(x = N, y = ratio_3)) +
  geom_hline(yintercept = 0.5, 
             linetype = "dashed") +
  geom_line(color = "dodgerblue") +
  labs(x = "試行回数", 
       y = "表の割合")  
plot(p3)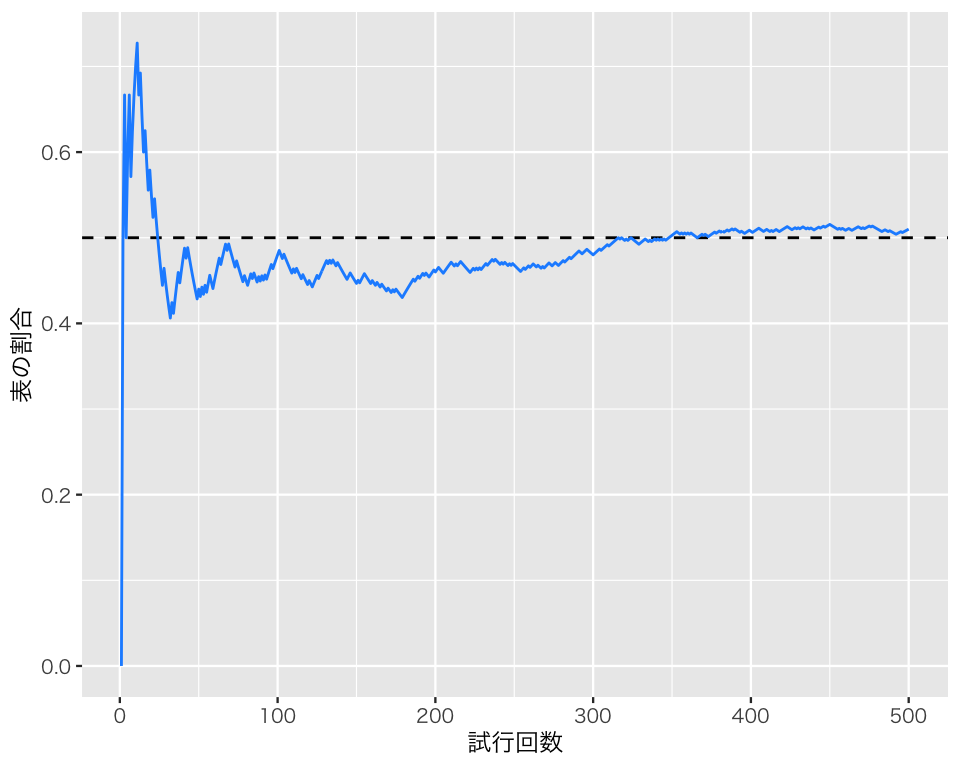

シミュレーションを実行する度に、異なる軌跡を描きながら、比率が0.5に近づいていく様子が見てとれる。

7.3 実習課題

  • コイン投げの回数 n_flips を減らしたり増やしたりして、シミュレーションを行ってみよう。
  • 表が出る確率 \(\theta = 0.8\), 裏が出る確率 \(1-\theta = 0.2\)として、同様のシミュレーションを実行してみよう。