6  母集団と標本をシミュレーションで理解する

今回の目標

6.1 準備

必要なパッケージを読み込む。

library(tidyverse)

## 図のなかで日本語を使えるようにする
## フォントの設定はお好みで
## （Unix/Linux ではIPAexフォントのインストールが必要かも）
if (.Platform$OS.type == "windows") { # Windows
  library(fontregisterer)
  my_font <- "Yu Gothic"
} else if (capabilities("aqua")) { # macOS
  my_font <- "HiraginoSans-W3"
} else { # Unix/Linux
  my_font <- "IPAexGothic"
}
theme_set(theme_gray(base_size = 9,
                     base_family = my_font))

6.2 母集団と標本のシミュレーション

6.2.1 母集団を用意する

例として、女性4,600人、男性5,400人から成る母集団を考える。合計10,000人で、女性比率が0.46、男性比率は0.54である。これらは母集団の比率なので、母比率と呼ばれる。

この母集団 (population) をRで定義しよう。

pop <- rep(c("female", "male"), c(4600, 5400))

総人口を確認する。

length(pop)
[1] 10000

男女の数を確認する。

table(pop)
pop
female   male 
  4600   5400

例題どおりの母集団が定義できた。

ここで、私たちは母比率を知らないと仮定しよう。 正しい母比率を調べるもっとも単純な方法は、1万人全員の性別を調べることである。しかし、1万人を調査するのは大変なので、1万人から100人だけを無作為に（ランダムに）選び、100人の性別を調べ、その結果を利用して母比率を推定することにする。

6.2.2 母集団から100人をランダムに選ぶ

上で定義した母集団から、ランダムに100人を抜き出してみよう。

sample() でランダムに100人抽出すればよい。同じ人物を2度以上抜き出すことがないよう、replace = FALSE で非復元抽出を指定する。また、標本サイズ \(N\) は繰り返し使うので、最初に定義しておく。

N <- 100
sample_1 <- sample(pop, size = N, replace = FALSE)

取り出した\(N=100\)のサンプルで、男女の比率を調べてみよう。

table(sample_1) / N
sample_1
female   male 
  0.43   0.57

この比率は標本（サンプル）の比率なので、標本比率と呼ばれる。 女性比率だけを調べる（女性比率がわかれば男性比率もわかるので）には、

sum(sample_1 == "female") / N
[1] 0.43

または、

mean(sample_1 == "female")
[1] 0.43

とすればよい。

もう一度、別の100人で調べてみよう（先ほどと同じ人物が選ばれる可能性はある）。

sample_2 <- sample(pop, size = N, replace = FALSE)
mean(sample_2 == "female")
[1] 0.48

もう一度、別の100人で調べてみよう（先ほどと同じ人物が選ばれる可能性はある）。

sample_3 <- sample(pop, size = N, replace = FALSE)
mean(sample_3 == "female")
[1] 0.45

このように、毎回異なる標本が抽出され、その結果として異なる標本比率が得られる。標本から得られる統計量は、母数（この例題の場合は母比率）と必ずしも一致しないし、同じ方法を何度も繰り返すと異なる値が得られる。

1万人から100人を選ぶ方法は \(6.5 \times 10^{241}\) 通りあるので、全部の組み合わせを調べるのは不可能である。そこで、Rを使って10,000通りだけ調べてみよう。

まず、1万個の結果（女性の標本比率）を保存する容器（ベクトル, vector）を用意する。

res_1 <- rep(NA, 1e4)

NA は欠測値（値がないこと）を表す。まだ結果を得ていないので、欠測値が1万個ある「空の」容器を用意した。

Tip

1e4 というのは、\(1 \times 10^4\) すなわち 10000 のことである。 この例のように、コンピュータでは桁が大きい数を e （プログラムによっては大文字の E）を用いて表すので覚えておこう。この e は自然対数の底（ネイピア数）ではないので注意。 Rでのネイピア数は exp(1) である。

確認のため、最初の10個分だけ表示してみよう。

res_1[1:10]
 [1] NA NA NA NA NA NA NA NA NA NA

すべて NA である。

次に、forループ を使って標本抽出（サンプリング）と母比率の計算を1万回実行する。\(i\)番目の結果は、res_1 の \(i\)番目の値として保存する。res_1の\(i\) 番目は res_1[i] と書く。

for (i in 1 : 1e4) {
  x <- sample(pop, size = N, replace = FALSE)
  res_1[i] <- mean(x == "female")
}

これで、結果が res_1 に保存された。確認のため、最初の10個の結果を表示してみよう。

res_1[1 : 10]
 [1] 0.49 0.46 0.47 0.48 0.40 0.46 0.45 0.50 0.46 0.46

さきほどは NA だったところに数値（標本比率）が保存されたことがわかる。

結果をヒストグラムにしてみよう。私たちは母比率を知っているので、母比率である0.46を赤い線で示す。

df1 <- tibble(sample = res_1)
hist1 <- ggplot(df1, aes(x = sample)) +
  geom_histogram(binwidth = 0.02, 
                 color = "black", 
                 fill = "dodgerblue") +
  geom_vline(xintercept = 0.46, 
             color = "red", 
             linewidth = 1.5) +
  labs(x = "女性の標本比率", 
       y = "度数")
plot(hist1)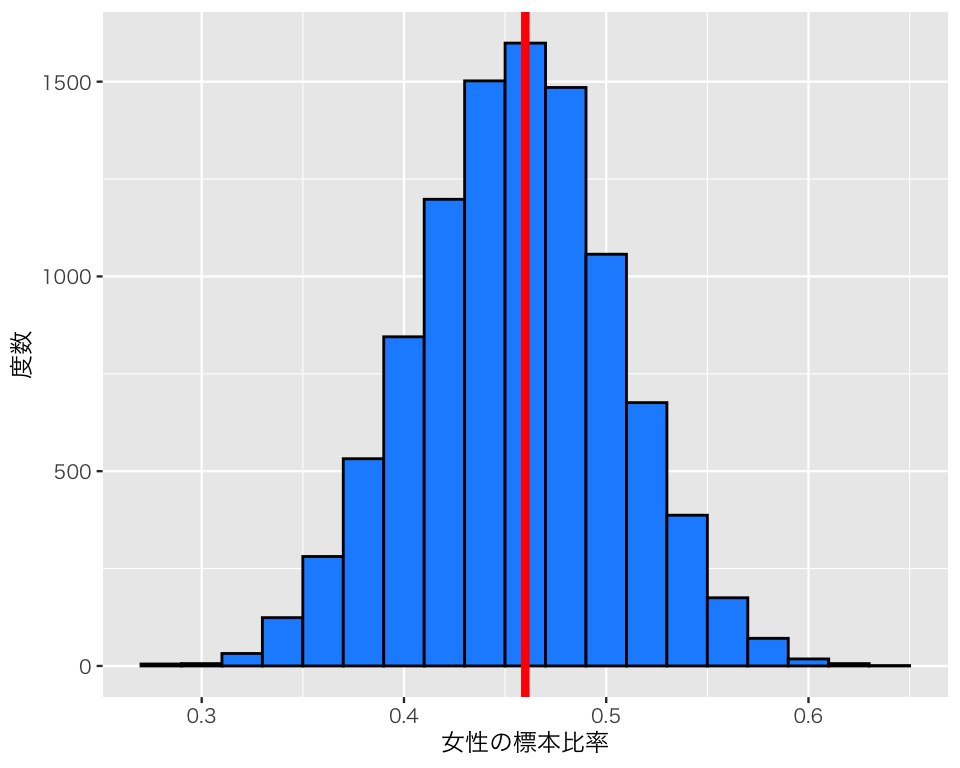

ヒストグラムを見ると、一つひとつの標本比率は母比率よりも大きかったり、母比率よりも小さかったりすることがわかる。しかし、平均すると母比率に近い値を得ることができそうだ。

このヒストグラムからわかる通り、統計量は分布する（つまり、標本ごとにばらばらの値をとる）。このような標本ごとの分布を 標本分布 (sampling distribution) と呼ぶ（標本分布については、次のトピックで説明する）。

6.2.3 標準誤差 (standard error; SE)

標本分布に現れる標準偏差（統計量のばらつき）を標準誤差 (standard error; SE) という。このシミュレーションで得られる標準誤差は、

sd(res_1)
[1] 0.04964357

である。

詳しくは次のトピックで説明するが、理論的には \[\mbox{SE} = \frac{母標準偏差}{\sqrt{標本サイズ}}\] なので、

pi <- 0.46
pop_sd <- sqrt(pi * (1 - pi))
pop_sd / sqrt(100)
[1] 0.04983974

になるはずであるが、シミュレーションなので実行する度に値が変わり、理論値に近づいたり離れたりする。

6.3 実習課題

標本サイズ \(N\) の値を変えて (\(N = 25\), \(N = 400\) で)、同様のシミュレーションを実行してみよう。

  • ヒストグラムはどのように変化するだろうか。
  • 標準誤差はどのように変化するだろうか。